Dilute oriented loop models Article Swipe
YOU?
·
· 2016
· Open Access
·
· DOI: https://doi.org/10.1088/1751-8113/49/6/064002
· OA: W2228732104
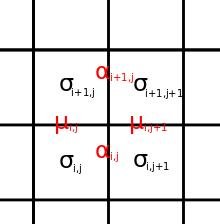
We study a model of dilute oriented loops on the square lattice, where each\nloop is compatible with a fixed, alternating orientation of the lattice edges.\nThis implies that loop strands are not allowed to go straight at vertices, and\nresults in an enhancement of the usual O(n) symmetry to U(n). The corresponding\ntransfer matrix acts on a number of representations (standard modules) that\ngrows exponentially with the system size. We derive their dimension and those\nof the centraliser by both combinatorial and algebraic techniques. A mapping\nonto a field theory permits us to identify the conformal field theory governing\nthe critical range, $n \\le 1$. We establish the phase diagram and the critical\nexponents of low-energy excitations. For generic n, there is a critical line in\nthe universality class of the dilute O(2n) model, terminating in an SU(n+1)\npoint. The case n=1 maps onto the critical line of the six-vertex model, along\nwhich exponents vary continuously.\n
