Measurable circle squaring Article Swipe

View

Related Concepts

Mathematics Lebesgue measure Partition (number theory) Bounded function Lebesgue integration Measure (data warehouse) Boundary (topology) Null set Pure mathematics Zero (linguistics) Dimension (graph theory) Discrete mathematics Set (abstract data type) Combinatorics Mathematical analysis Computer science Philosophy Programming language Linguistics Database

Łukasz Grabowski , András Máthé , Oleg Pikhurko ·

YOU? · · 2017 · Open Access · · DOI: https://doi.org/10.4007/annals.2017.185.2.6 · OA: W253921512

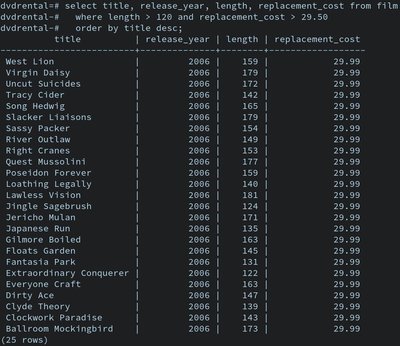
Laczkovich proved that if bounded subsets $A$ and $B$ of $R^k$ have the same non-zero Lebesgue measure and the box dimension of the boundary of each set is less than $k$, then there is a partition of $A$ into finitely many parts that can be translated to form a partition of $B$. Here we show that it can be additionally required that each part is both Baire and Lebesgue measurable. As special cases, this gives measurable and translation-only versions of Tarski's circle squaring and Hilbert's third problem.