Parameterized Complexity of 1-Planarity Article Swipe

View

Related Concepts

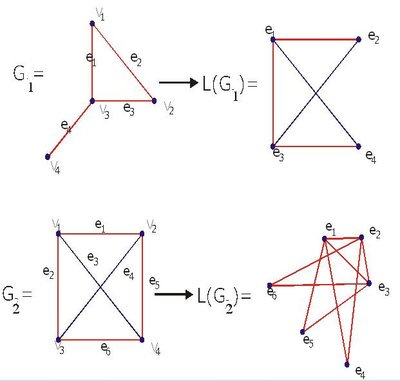
Parameterized complexity Treewidth Pathwidth Vertex cover Planar graph Combinatorics Mathematics Planarity testing Bounded function Book embedding Discrete mathematics Planar 1-planar graph Computer science Graph Chordal graph Line graph Mathematical analysis Computer graphics (images)

Michael J. Bannister , Sergio Cabello , David Eppstein ·

YOU? · · 2017 · Open Access · · DOI: https://doi.org/10.7155/jgaa.00457 · OA: W2772525715

We consider the problem of drawing graphs with at most one crossing per edge. These drawings, and the graphs that can be drawn in this way, are called $1$-planar. Finding $1$-planar drawings is known to be ${\mathsf{NP}}$-hard, but we prove that it is fixed-parameter tractable with respect to the vertex cover number, tree-depth, and cyclomatic number. Special cases of these algorithms provide polynomial-time recognition algorithms for $1$-planar split graphs and $1$-planar cographs. However, recognizing $1$-planar graphs remains ${\mathsf{NP}}$-complete for graphs of bounded bandwidth, pathwidth, or treewidth.