Dynamical analysis on $f(R, \mathcal{G})$ cosmology Article Swipe

View

Related Concepts

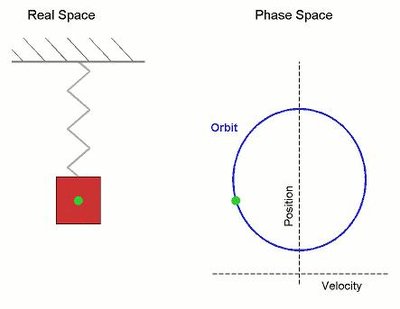
Physics Attractor Cosmology Phase space Formalism (music) Epoch (astronomy) Ordinary differential equation Dynamical systems theory Class (philosophy) Cosmological model Mathematical physics Differential equation Gravitation Theoretical physics Dynamical system (definition) Classical mechanics Mathematical analysis Astrophysics Quantum mechanics Mathematics Art Artificial intelligence Stars Computer science Musical Visual arts

S. Santos da Costa , F. Roig , J. S. Alcaniz , Salvatore Capozzıello , Mariafelicia De Laurentis , Micol Benetti ·

YOU? · · 2018 · Open Access · · DOI: https://doi.org/10.1088/1361-6382/aaad80 · OA: W2787727992

We use a dynamical system approach to study the cosmological viability of\n$f(R,\\mathcal{G})$ gravity theories. The method consists of formulating the\nevolution equations as an autonomous system of ODEs, using suitable variables.\nThe formalism is applied to a class of models in which $f(R,\\mathcal{G})\\propto\nR^{n}\\mathcal{G}^{1-n}$ and its solutions and corresponding stability are\nanalysed in detail. New accelerating solutions that can be attractors in the\nphase space are found. We also find that this class of models does not exhibit\na matter-dominated epoch, a solution which is inconsistent with current\ncosmological observations.\n