On arbitrarily slow convergence rates for strong numerical approximations of Cox-Ingersoll-Ross processes and squared Bessel processes Article Swipe
YOU?
·
· 2017
· Open Access
·
· DOI: https://doi.org/10.48550/arxiv.1702.08761
· OA: W2949112389
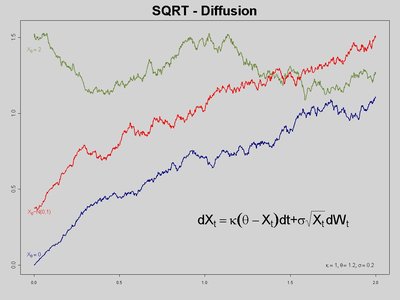
Cox-Ingersoll-Ross (CIR) processes are extensively used in state-of-the-art models for the approximative pricing of financial derivatives. In particular, CIR processes are day after day employed to model instantaneous variances (squared volatilities) of foreign exchange rates and stock prices in Heston-type models and they are also intensively used to model short-rate interest rates. The prices of the financial derivatives in the above mentioned models are very often approximately computed by means of explicit or implicit Euler- or Milstein-type discretization methods based on equidistant evaluations of the driving noise processes. In this article we study the strong convergence speeds of all such discretization methods. More specifically, the main result of this article reveals that each such discretization method achieves at most a strong convergence order of $δ/2$, where $0
