Asymptotic properties of maximum likelihood estimator for the growth rate of a stable CIR process based on continuous time observations Article Swipe

View

Related Concepts

Mathematics Asymptotic distribution Estimator Consistency (knowledge bases) Applied mathematics Strong consistency Asymptotic analysis Supercritical fluid Wiener process Cox–Ingersoll–Ross model Statistics Discrete mathematics Interest rate Monetary economics Chemistry Organic chemistry Economics

Mátyás Barczy , Mohamed Ben Alaya , Ahmed Kebaier , Gyula Pap ·

YOU? · · 2019 · Open Access · · DOI: https://doi.org/10.1080/02331888.2019.1579216 · OA: W2962989798

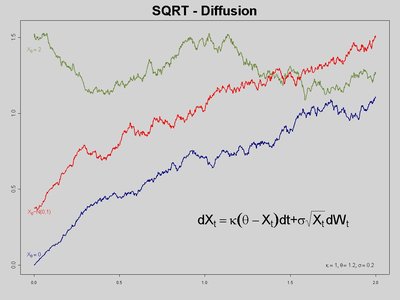
We consider a stable Cox--Ingersoll--Ross process driven by a standard Wiener\nprocess and a spectrally positive strictly stable L\\'evy process, and we study\nasymptotic properties of the maximum likelihood estimator (MLE) for its growth\nrate based on continuous time observations. We distinguish three cases:\nsubcritical, critical and supercritical. In all cases we prove strong\nconsistency of the MLE in question, in the subcritical case asymptotic\nnormality, and in the supercritical case asymptotic mixed normality are shown\nas well. In the critical case the description of the asymptotic behavior of the\nMLE in question remains open.\n