Gibbs–Wilbraham phenomenon on Lagrange interpolation based on analytic weights on the unit circle Article Swipe

View

Related Concepts

Mathematics Lagrange polynomial Interpolation (computer graphics) Unit circle Gibbs phenomenon Convergence (economics) Applied mathematics Trigonometric interpolation Unit (ring theory) Constraint algorithm Mathematical analysis Polynomial interpolation Lagrange multiplier Mathematical optimization Linear interpolation Polynomial Fourier series Animation Economic growth Computer science Computer graphics (images) Mathematics education Economics

E. Berriochoa , A. Cachafeiro , J.M. García Amor ·

YOU? · · 2019 · Open Access · · DOI: https://doi.org/10.1016/j.cam.2019.112376 · OA: W2966178308

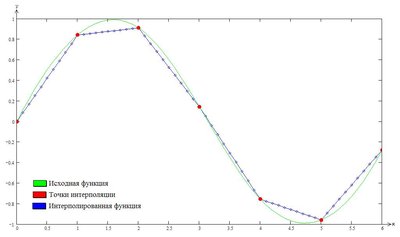
This paper is devoted to study Lagrange interpolation based on nodal systems constituted by the roots of para-orthogonal polynomials with respect to analytic weights on the unit circle. The presented results address, in addition to algorithmic and convergence questions for continuous and discontinuous functions, a detailed study of the Gibbs-Wilbraham phenomenon.