Approximation by Szasz-Mirakjan-Durrmeyer operators based on shape parameter $\lambda$ Article Swipe

PDF

Related Concepts

Mathematics Modulus of continuity Lipschitz continuity Type (biology) Convergence (economics) Lambda Mathematical analysis Asymptotic formula Applied mathematics Order (exchange) Rate of convergence Pure mathematics Channel (broadcasting) Finance Ecology Physics Economics Economic growth Engineering Biology Electrical engineering Optics

Reşat Aslan ·

YOU? · · 2022 · Open Access · · DOI: https://doi.org/10.31801/cfsuasmas.941919 · OA: W4281684643

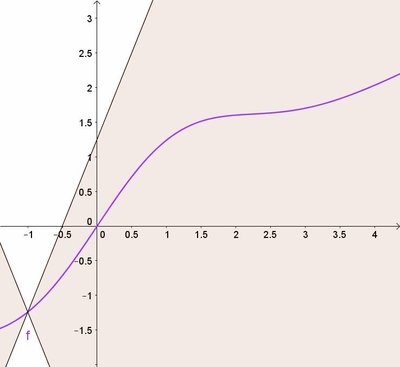
In this paper, we study several approximation properties of Szasz-Mirakjan-Durrmeyer operators with shape parameter λ∈[−1,1]λ∈[−1,1]. Firstly, we obtain some preliminaries results such as moments and central moments. Next, we estimate the order of convergence in terms of the usual modulus of continuity, for the functions belong to Lipschitz type class and Peetre's K-functional, respectively. Also, we prove a Korovkin type approximation theorem on weighted spaces and derive a Voronovskaya type asymptotic theorem for these operators. Finally, we give the comparison of the convergence of these newly defined operators to the certain functions with some graphics and error of approximation table.