The interlace polynomial of binary delta-matroids and link invariants Article Swipe
Related Concepts
Matroid
Invariant (physics)
Mathematics
Combinatorics
Chromatic polynomial
Graphic matroid
Dual graph
Polynomial
Tutte polynomial
Binary number
Discrete mathematics
Generalization
Graph
Planar graph
Arithmetic
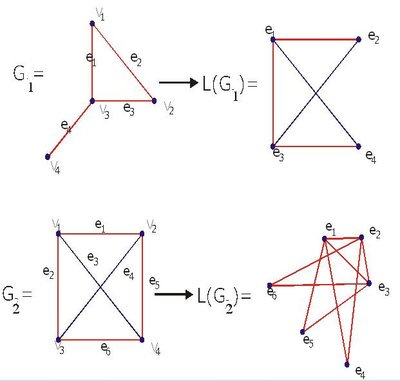
Line graph
Voltage graph
Mathematical analysis
Mathematical physics
Nadezhda Kodaneva
·
 YOU?
·
· 2020
· Open Access
·
· DOI: https://doi.org/10.48550/arxiv.2002.12440
· OA: W4287863841
YOU?
·
· 2020
· Open Access
·
· DOI: https://doi.org/10.48550/arxiv.2002.12440
· OA: W4287863841
 YOU?
·
· 2020
· Open Access
·
· DOI: https://doi.org/10.48550/arxiv.2002.12440
· OA: W4287863841
YOU?
·
· 2020
· Open Access
·
· DOI: https://doi.org/10.48550/arxiv.2002.12440
· OA: W4287863841
In this work, we study the interlace polynomial as a generalization of a graph invariant to delta-matroids. We prove that the interlace polynomial satisfies the four-term relation for delta-matroids and determines thus a finite type invariant of links in the 3-sphere.
Related Topics
Finding more related topics…