Normal Higher-Order Termination Article Swipe

View

Related Concepts

Rewriting Reduction (mathematics) Mathematics Type (biology) Extension (predicate logic) Order (exchange) Base (topology) Algebraic number Dependent type Calculus (dental) Algebra over a field Pure mathematics Discrete mathematics Lambda calculus Computer science Programming language Mathematical analysis Geometry Economics Ecology Finance Biology Medicine Dentistry

Jean-Pierre Jouannaud , Albert Rubio ·

YOU? · · 2015 · Open Access · · DOI: https://doi.org/10.1145/2699913 · OA: W2137965931

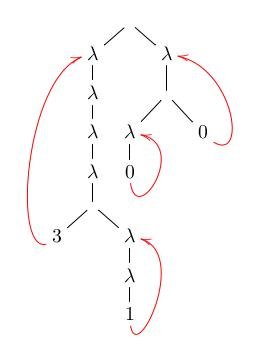
We extend the termination proof methods based on reduction orderings to higher-order rewriting systems based on higher-order pattern matching. We accommodate, on the one hand, a weakly polymorphic, algebraic extension of Church’s simply typed λ-calculus and, on the other hand, any use of eta, as a reduction, as an expansion, or as an equation. The user’s rules may be of any type in this type system, either a base, functional, or weakly polymorphic type.