Eulerian Cycle Decomposition Conjecture for the line graph of complete graphs

YOU? · · 2018 · Open Access · · DOI: https://doi.org/10.1016/j.akcej.2018.01.012

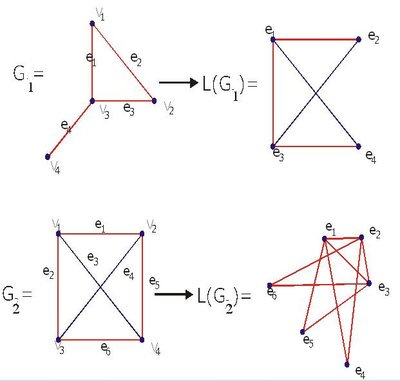
The Eulerian Cycle Decomposition Conjecture, by Chartrand, Jordon and Zhang, states that if the minimum number of odd cycles in a cycle decomposition of an Eulerian graph of size is the maximum number of odd cycles in such a cycle decomposition is and is an integer such that where and are of the same parity, then there is a cycle decomposition of with exactly odd cycles. This conjecture is verified for the line graph of the complete graph.

Concepts

Mathematics Eulerian path Combinatorics Conjecture Graph Cycle basis Discrete mathematics Decomposition Line graph Graph power Pure mathematics Chemistry Lagrangian Organic chemistry

Metadata

Type: article
Language: en
Landing Page: https://doi.org/10.1016/j.akcej.2018.01.012
PDF: https://www.tandfonline.com/doi/pdf/10.1016/j.akcej.2018.01.012?needAccess=true
OA Status: gold
Cited By: 1
References: 5
Related Works: 10
OpenAlex ID: https://openalex.org/W2793107901

All OpenAlex metadata

Raw OpenAlex JSON

No additional metadata available.

Eulerian Cycle Decomposition Conjecture for the line graph of complete graphs Article Swipe

Related Topics To Compare & Contrast

Raw OpenAlex JSON