Alternative way to derive the distribution of the multivariate Ornstein–Uhlenbeck process Article Swipe

PDF

Related Concepts

ornstein–uhlenbeck process mathematics applied mathematics probability density function multivariate normal distribution covariance inverse-wishart distribution matrix normal distribution multivariate statistics moment-generating function normal-wishart distribution covariance matrix statistical physics mathematical analysis stochastic process statistics physics

Pat Vatiwutipong , Nattakorn Phewchean ·

YOU? · · 2019 · Open Access · · DOI: https://doi.org/10.1186/s13662-019-2214-1 · OA: W2957292769

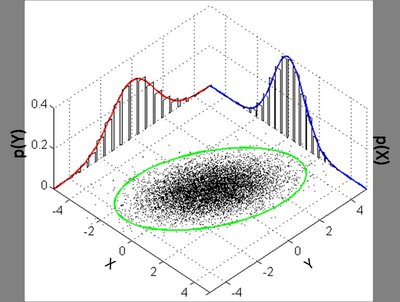
In this paper, we solve the Fokker–Planck equation of the multivariate Ornstein–Uhlenbeck process to obtain its probability density function. This approach allows us to ascertain the distribution without solving it analytically. We find that, at any moment in time, the process has a multivariate normal distribution. We obtain explicit formulae of mean, covariance, and cross-covariance matrix. Moreover, we obtain its mean-reverting condition and the long-term distribution.