Description
In mathematics, a group action of a group G {\displaystyle G} on a set S {\displaystyle S} is a group homomorphism from G {\displaystyle G} to some group (under function composition) of functions from S {\displaystyle S} to itself. It is said that G {\displaystyle G} acts on S {\displaystyle S} .
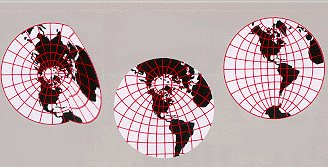
Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles.
If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in it; in particular, it acts on the set of all triangles. Similarly, the group of symmetries of a polyhedron acts on the vertices, the edges, and the faces of the polyhedron.
A group action on a vector space is called a representation of the group. In the case of a finite-dimensional vector space, it allows one to identify many groups with subgroups of the general linear group GL ( n , K ) {\displaystyle \operatorname {GL} (n,K)} , the group of the invertible matrices of dimension n {\displaystyle n} over a field K {\displaystyle K} .
The symmetric group S n {\displaystyle S_{n}} acts on any set with n {\displaystyle n} elements by permuting the elements of the set. Although the group of all permutations of a set depends formally on the set, the concept of group action allows one to consider a single group for studying the permutations of all sets with the same cardinality.
Group Action News
Tags
Collections
No collections available for this topic.