Quasiconvex Function
Swipe Quasiconvex Function Vs...
Quasiconvex Function News
Description
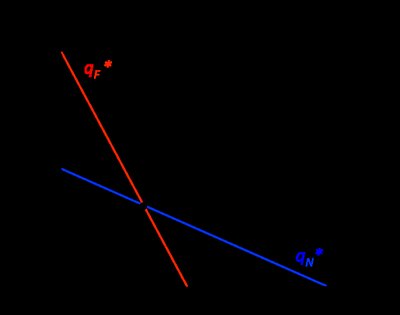
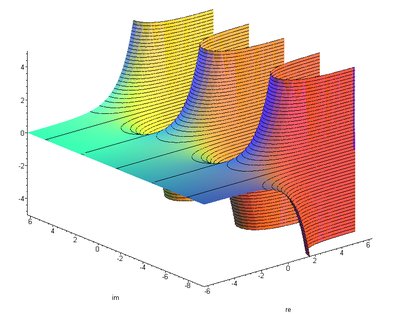
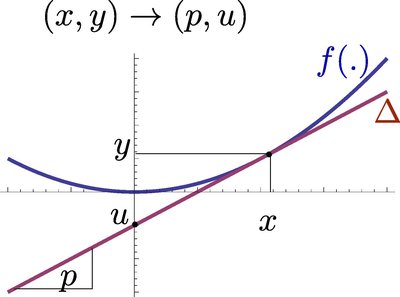
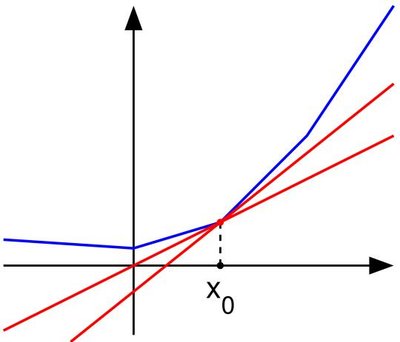
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form ( − ∞ , a ) {\displaystyle (-\infty ,a)} is a convex set. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.
All convex functions are also quasiconvex, but not all quasiconvex functions are convex, so quasiconvexity is a generalization of convexity. Univariate unimodal functions are quasiconvex or quasiconcave, however this is not necessarily the case for functions with multiple arguments. For example, the 2-dimensional Rosenbrock function is unimodal but not quasiconvex and functions with star-convex sublevel sets can be unimodal without being quasiconvex.
Related
More
Collections
No collections available for this topic.
Details
- Slug: quasiconvex-function
- Added: Jul 20, 2024