Description
In mathematics and physics, the right-hand rule is a convention and a mnemonic for deciding the orientation of axes in three-dimensional space. It is a convenient method for determining the direction of the cross product of two vectors.
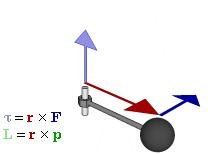
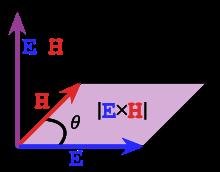
There are two ways of applying the right hand rule. The first one is conventionally called the Right hand rule or the Flemming's right hand rule. It involves the index finger, the middle finger and the thumb of the right hand. By arranging them as shown in the diagram, the direction of cross product or vector product can be calculated.
The other way, known as Amperes right hand grip rule, right-hand screw rule , coffee-mug rule or the corkscrew-rule involves pointing all fingers of the right hand along the first vector and curling the fingers along the second vector, the direction which the thumb makes is the direction of vector product.
For example, If the curling motion of the fingers represents a movement from the first ( x -axis) to the second ( y -axis), then the third ( z -axis) can point along either thumb in a right handed coordinate system.
Both these rules can be used interchangeably.
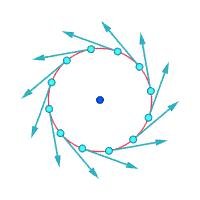
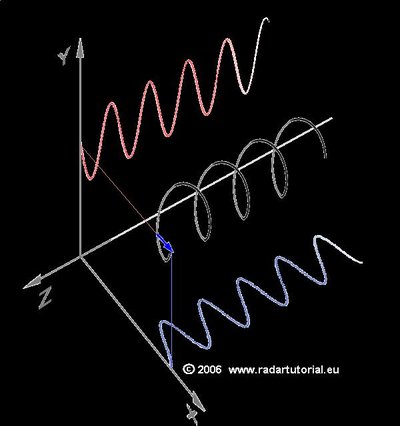
The rule can be used to find the direction of the magnetic field, rotation, spirals, electromagnetic fields, mirror images, and enantiomers in mathematics and chemistry.
The sequence is often: index finger along the first vector, then middle finger along the second, then thumb along the third. Two other sequences also work because they preserve the cyclic nature of the cross product (and the underlying Levi-Civita symbol):
- Middle finger, thumb, index finger.
- Thumb, index finger, middle finger.
Right-Hand Rule News
Tags
Collections
No collections available for this topic.