Description
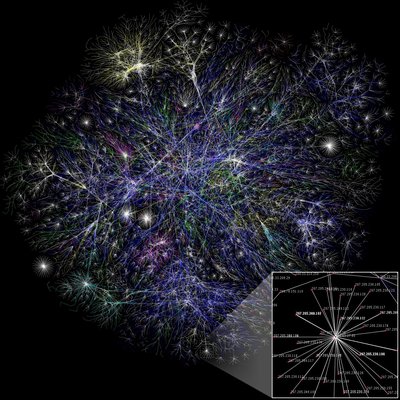
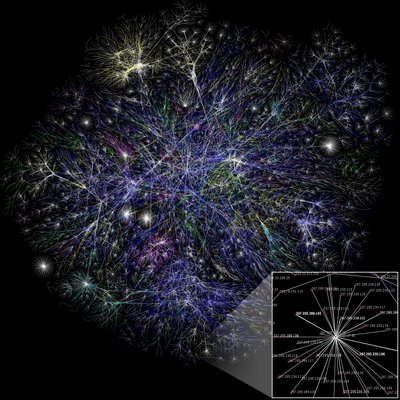
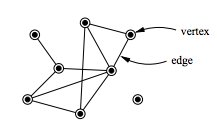
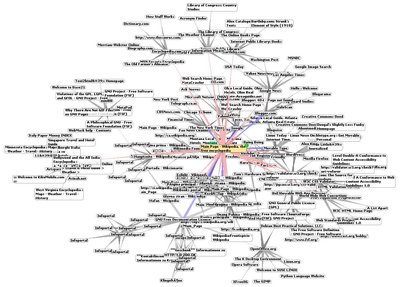
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as
P ( k ) ∼ k − γ {\displaystyle P(k)\ \sim \ k^{\boldsymbol {-\gamma }}}
where γ {\displaystyle \gamma } is a parameter whose value is typically in the range 2 < γ < 3 {\textstyle 2<\gamma <3} (wherein the second moment (scale parameter) of k − γ {\displaystyle k^{\boldsymbol {-\gamma }}} is infinite but the first moment is finite), although occasionally it may lie outside these bounds. The name "scale-free" could be explained by the fact that some moments of the degree distribution are not defined, so that the network does not have a characteristic scale or "size".
Preferential attachment and the fitness model have been proposed as mechanisms to explain the power law degree distributions in real networks. Alternative models such as super-linear preferential attachment and second-neighbour preferential attachment may appear to generate transient scale-free networks, but the degree distribution deviates from a power law as networks become very large.
Scale-Free Network News
Tags
Collections
No collections available for this topic.