Description
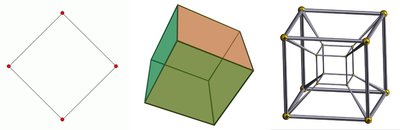
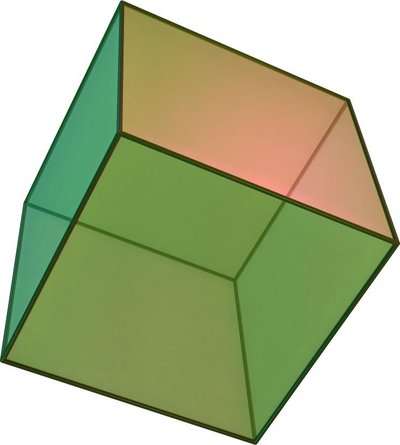
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.
The tesseract is also called an 8-cell , C 8, (regular) octachoron , octahedroid , cubic prism , and tetracube. It is the four- dimensional hypercube , or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the γ 4 {\displaystyle \gamma {4}} polytope. The term _hypercube without a dimension reference is frequently treated as a synonym for this specific polytope.
The Oxford English Dictionary traces the word tesseract to Charles Howard Hinton's 1888 book A New Era of Thought. The term derives from the Greek téssara (τέσσαρα 'four') and aktís (ἀκτίς 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled the word as tessaract.