Vector Projection

Swipe Vector Projection Vs...

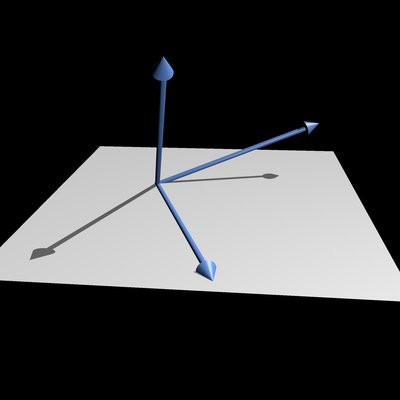
The vector projection (also known as the vector component or vector resolution ) of a vector a on (or onto) a nonzero vector b is the orthogonal projection of a onto a straight line parallel to b. The projection of a onto b is often written as proj b ⁡ a {\displaystyle \operatorname {proj} _{\mathbf {b} }\mathbf {a} } or a ∥ b.

The vector component or vector resolute of a perpendicular to b , sometimes also called the vector rejection of a from b (denoted oproj b ⁡ a {\displaystyle \operatorname {oproj} {\mathbf {b} }\mathbf {a} } or a ⊥ b ), is the orthogonal projection of a onto the plane (or, in general, hyperplane) that is orthogonal to b. Since both proj b ⁡ a {\displaystyle \operatorname {proj} {\mathbf {b} }\mathbf {a} } and oproj b ⁡ a {\displaystyle \operatorname {oproj} _{\mathbf {b} }\mathbf {a} } are vectors, and their sum is equal to a , the rejection of a from b is given by:

To simplify notation, this article defines a 1 := proj b ⁡ a {\displaystyle \mathbf {a} {1}:=\operatorname {proj} {\mathbf {b} }\mathbf {a} } and a 2 := oproj b ⁡ a . {\displaystyle \mathbf {a} {2}:=\operatorname {oproj} {\mathbf {b} }\mathbf {a} .} Thus, the vector a 1 {\displaystyle \mathbf {a} {1}} is parallel to b , {\displaystyle \mathbf {b} ,} the vector a 2 {\displaystyle \mathbf {a} {2}} is orthogonal to b , {\displaystyle \mathbf {b} ,} and a = a 1 + a 2 . {\displaystyle \mathbf {a} =\mathbf {a} {1}+\mathbf {a} {2}.}

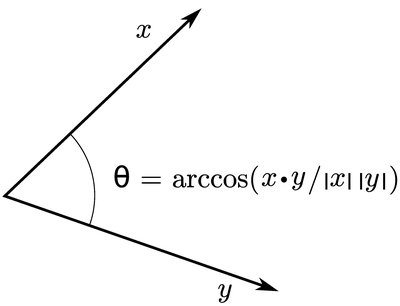
The projection of a onto b can be decomposed into a direction and a scalar magnitude by writting it as a 1 = a 1 b ^ {\displaystyle \mathbf {a} {1}=a{1}\mathbf {\hat {b}} } where a 1 {\displaystyle a_{1}} is a scalar, called the scalar projection of a onto b , and b̂ is the unit vector in the direction of b. The scalar projection is defined as

where the operator ⋅ denotes a dot product, ‖ a ‖ is the length of a , and θ is the angle between a and b. The scalar projection is equal in absolute value to the length of the vector projection, with a minus sign if the direction of the projection is opposite to the direction of b , that is, if the angle between the vectors is more than 90 degrees.

The vector projection can be calculated using the dot product of a {\displaystyle \mathbf {a} } and b {\displaystyle \mathbf {b} } as: